GEOMETRÍA PLANA: IGUALDAD, SEMEJANZA, SIMETRÍA, PROPORCIONALIDAD Y EQUIVALENCIA.

DESCÁRGATE LOS APUNTES EN PDF AQUÍ


EXTRAIDO DE LA PÁGINA WEB: http://dibujo.ramondelaguila.com/?page_id=2320#igualdad

1) Igualdad.

Dos figuras son iguales cuando tienen sus lados iguales y sus ángulos iguales, de tal forma que si se superponen coinciden.

Construcción de figuras iguales.

a) Descomposición en triángulos.( método de triangulación). Fig. A

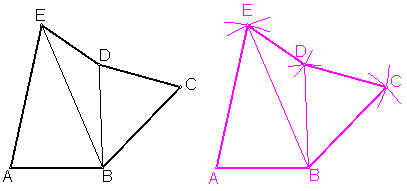
Fig. A

Es el método más preciso, ya que consiste en trasladar triángulos..

.- Descomponemos la figura en tres triángulos.
.- Llevamos sobre una recta uno de los lados por ejemplo el AB.
.- Construimos el triángulo ABE = A’B’E’.
.- Completamos el ejercicio construyendo los triángulosBDE = B’D’E’ y BCD = B’C’D’





b) Construcción de una figura igual a otra por el método de ángulos. Fig. B.

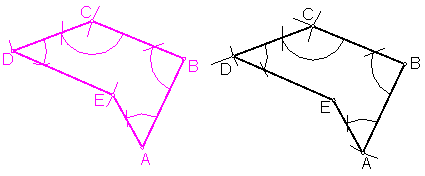
Fig. B

Al utilizar el compás para el traslado de los ángulos, este método es menos preciso que el anterior.

Sea la figura ABCDE.

Consiste en transportar los ángulos y los segmentos que componen el polígono.

c) Construcción de una figura igual a otra por el método de coordenadas.Sea el polígono ABCD. Fig. C.

Sea el polígono ABCD.

Hacemos pasar una recta cualquiera por el vértice A.

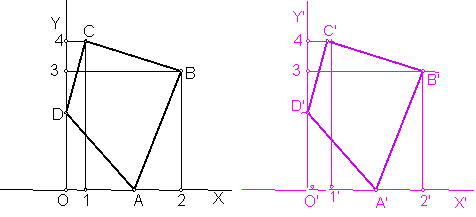
Fig. C

Partiendo de la figura original, se trazan los ejes X e Y, haciéndolos coincidir con los vértices D y A.
Se trazan perpendiculares al eje X por los vértices restantesC y B, hasta obtener los puntos,O, 1, 2,
Para construir la figura se dibujan dos ejes coordenados X e Y.
Sobre el eje X, y haciendo uso del compás, se llevan los puntos obtenidos O’,1’,A’, 2’
Levantamos perpendiculares al eje X, y obre ellas, se llevan las coordenadas, O’D’, 1’C’, 2’B’

d) Construcción de una figura igual a otra por radiación. Fig. D.

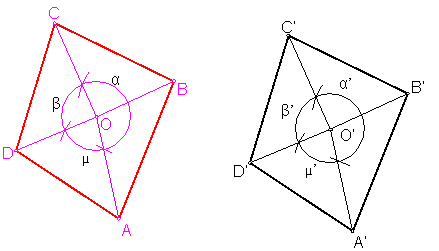
Fig. D

Sea la figura ABCD.

Elegimos un punto cualquiera O de la figuraABCD.

Unimos todos los vértices con dicho punto.

Elegimos otro punto cualquiera O’ y trasladamos los ángulosα, β, µ.

Medimos los segmentosOA, OB etc. y los y trasladamos.

2) Semejanza

Dos figuras son semejantes, cuando teniendo el mismo número de lados, estos son proporcionales y los ángulos formados entre ellos son iguales.

La razón existente entre dos figuras semejantes se llama, razón de semejanza.

Un caso particular de semejanza es La Homotecia 

2B) HOMOTECIA

es una transformación geométrica plana, en la cual los puntos relacionados o transformados se denominan homotéticos, y cumplen las siguientes condiciones:

Los puntos homotéticos están alineados con un tercero fijo llamado centro de la Homotecia (O).

La relación entre los segmentos definidos por este centro y los puntos transformado y original es una constante denominada razón de la homotecia (k).

Dos figuras homotéticas guardan relación de semejanza.

El centro de la Homotecia es invariante, y las rectas que pasan por el centro de la Homotecia también lo son, aunque no lo son por puntos (los puntos no son dobles).

CASOS POSIBLES DE HOMOTECIA: 

• Si la constante k es mayor que 0, la Homotecia se denomina directa, y en ella los puntos homotéticos están ambos al mismo lado del centro de la Homotecia.
• Si la constante k es menor que 0, la Homotecia se denomina inversa, y en ella los puntos homotéticos están en lados diferentes con respecto al centro de la Homotecia.
• Si la constante k es 1, la figura homotética coincide con la original, y la transformación se denomina Función Identidad.
• Si la constante k es -1, la Homotecia se convierte en una Simetría Central.
• Si el valor absoluto de la constante k es mayor que 1, la Homotecia produce un aumento de tamaño (la figura final es mayor que la original).
• Si el valor absoluto de la constante k es menor que 1, la Homotecia produce una disminución de tamaño (la figura final es menor que la original).
• Dos rectas homotéticas siempre son paralelas, y la razón de longitud de dos segmentos homotéticos es igual a la razón de la homotecia (k).
• La Homotecia es una transformación plana reversible, esto es, si aplicamos una homotecia a una figura y después aplicamos una segunda homotecia de igual centro y con igual razón pero de diferente signo, obtenemos la figura original.
• Una Homotecia de centro impropio (en el infinito) es una Traslación.

A) Dada la poligonal A, B, C, D, E. y el centro de homotecia “O”. Hallar la figura semejante cuya razón de semejanza sea 1/2.

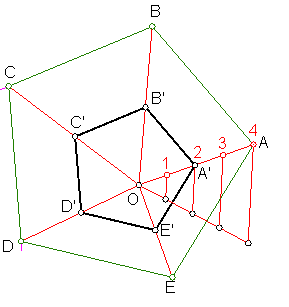
Se unen todos los vértices con el centro de homotecia “O”.

Uno de dichos segmentos se divide en tantas partes como indique el denominador, es decir DOS.

Seguidamente a partir de “O” se toman tantas divisiones como indique el numerador es decir, una.

Por el extremo de dicha  división se trazan paralelas a los lados  de la poligonal, obteniendo los vértices A’. B’. C’. D’, E’

a) Dada la poligonal A, B, C, D, E. y el centro de homotecia “O”. Hallar la figura semejante cuya razón de semejanza sea 3/5.

Se unen todos los vértices con el centro de homotecia  “O”.

Uno de dichos segmentos se divide en tantas partes como indique el denominador, es decir cinco.

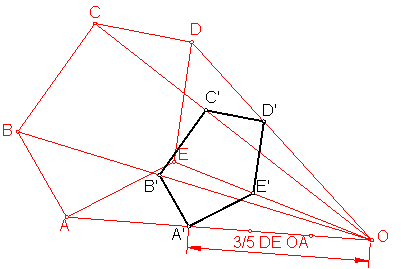
Seguidamente a partir de “O” se toman tantas divisiones como indique el numerador es decir, tres.

Por el extremo de dicha  división se trazan paralelas a los lados  de la poligonal, obteniendo los vértices A’. B’. C’. D’, E’

3) Simetría

Se dice que dos puntos son simétricos respecto a otro, tomado como centro, cuando estando contenidos en una recta que pasa por en punto centro, sus distancias al mismo son iguales.

En la figura los puntos B y B‘ son simétricos con respecto al centro O. 

Dos puntos son simétricos con respecto a un eje, cuando tomados sobre una perpendicular al mismo sus distancias son equidistantes. Fig. 2.

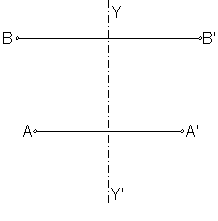
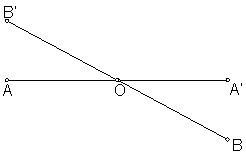
Fig. 2

Los puntos A y A’son simétricos con respecto al eje YY’.

Dos líneas son simétricas, cuando lo son todos sus puntos. Cuando se trata de segmentos rectilíneos bastará con que sean los extremos de los mismos.

Para trazar un segmento A’B’, simétrico de otro AB, bastará con trazar por los extremos de dichos segmentos rectas perpendiculares al eje YY’, y transportar las distancia que separa cada punto del eje. Fig. 3.

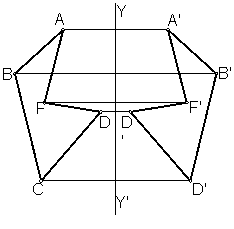
Fig. 3

Existen figuras en las que se dispone de varios ejes de simetría. En la figura el eje YY’ es un eje principal y el XX’ es secundario. Fig. 4.

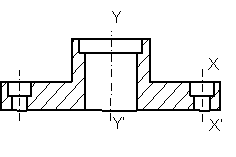
Fig. 4

4)Proporcionalidad.

a) Teorema de Thales

Si una familia de rectas paralelasr, s, t, son cortadas por dos rectas oblicuas a ellas, u, v, los segmentos en que estas últimas cortan a las primeras serán proporcionales. Fig. 1

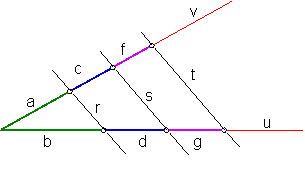
Fig. 1

a/b = c/d = f/g

b) División de un segmento en un número determinado de partes iguales. Fig. 2.

Sea el segmento AB.

En el extremo A se traza una recta con una inclinación arbitraria.

Sobre dicha recta se llevan tantas divisiones iguales y de longitud arbitraria como partes se quiera dividir el segmento AB, por ejemplo siete divisiones, 1’, 2’, 3’ etc. utilizando el compás.

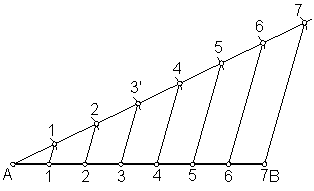
Fig. 2

Se une la ultima división 7 con el extremo B.

Seguidamente se trazan paralelas a la recta 7’ B por el resto de las divisiones.

Dichas paralelas nos determinan los puntos de división 1, 2, 3, 4 etc. del segmento AB.

c) Tercera proporcional de dos segmentos ( primer procedimiento). Fig. 1

Sean los segmentos a y b

Trazamos dos rectas cualquiera r y s.

Sobre un de ellas, por ejemplo la s, se llevan los segmentos a y b.

Fig. 1

Sobre la otra recta se lleva el segmento b.

Unimos el extremo de a con el extremo deb, recta u.

Por el extremo de b se traza una paralela a u hasta que corte a r.

El segmento x será la tercera proporcional.

d) Tercera proporcional de dos segmentos ( segundo procedimiento). Fig. 1

Trazamos dos rectas cualquiera r y s.

Por el extremo  A, llevamos los segmentosa y b.

Unimos el extremo de a con el extremo de b.

Haciendo centro en A, trazamos un arco que corte a la recta s en el punto B.

Por B trazamos una paralela a la recta anterior.

Fig. 1

El segmento x será la tercera proporcional buscada.

e) Cuarta proporcional de tres segmentos. Fig. 1.

Sean los segmentos a, b, y c.

A partir de A trazamos dos restas arbitrarias r y s.

Sobre una de las rectas, por ejemplo la r, llevamos los segmentos a y b.

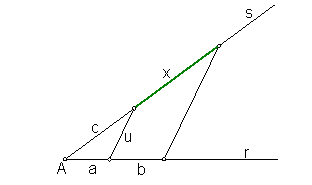
Fig. 1

Sobre la recta s, llevamos el segmento c.

Unimos los extremos a y c, recta u.

Por el extremo de b, trazamos una paralela a uhasta que corte a s.

El segmento x será la cuarta proporcional.

f) Dividir un segmento en partes proporcionales a otros. Fig. 1

Sean los segmentos AB, a, b, c, y d.

En el extremo de A, trazamos una recta arbitraria.

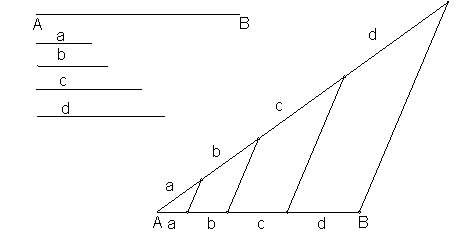
Fig. 1

Sobre el extremo A, llevamos los segmentos a,b, c y d, uno a continuación del otro.

Unimos la última división con el extremo B.

Por los extremos de a,b y c, trazamos paralela a la recta anterior, obteniendo los segmentos a’,b’,c’, d’,proporcionales a los dados.

MEDIO PROPORCIONAL

En una proporción continua, se denomina medio proporcional a cada uno de los términos iguales.

Para calcular el medio proporcional de una proporción continua se extrae la raíz cuadrada del producto de los extremos.

medio proporcional

g) Media proporcional de dos segmentos dados. ( primer procedimiento). Fig. 1.

Para su construcción aplicaremos el Teorema de Euclides, conocido también como Teorema de la Altura.

Este dice: La altura de un triángulo rectángulo respecto a la hipotenusa es media proporcional entre las proyecciones de los catetos sobre la misma.

a / x = x / b                x2  =  a * b

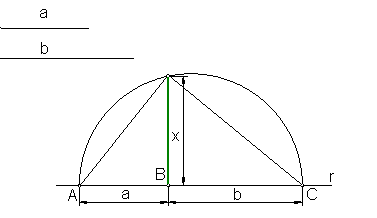
Fig. 1

Sean los segmentos a y b y una recta r cualquiera.

Elegimos un punto cualquiera de dicha recta por ejemplo A.

Llevamos a partir de dicho punto el segmento a y a continuación el b.

Hallamos la mediatriz del segmentoAC, y trazamos la semicircunferencia que pase  por dichos extremos de AB.

La perpendicular trazada por B nos determina el segmento x media proporcional buscada.

g) Media proporcional de dos segmentos dados. ( segundo procedimiento). Fig. 1
.

En este segundo procedimiento aplicaremos el Teorema del Cateto.

Este dice: En un triángulo rectángulo un cateto es media proporcional entre la hipotenusa y la proyección del mismo sobre ella. Fig. 131.

a / x = x / b                           x2  =  a * b

Fig. 1

Sean los segmentos a y b y una recta rcualquiera.

Elegimos un punto cualquiera de la recta  rpor ejemplo A.

A partir de A llevamos el segmento a y el b.

Trazamos la circunferencia que pase por A yB

Levantamos por C una perpendicular hasta que corte a la semicircunferencia en D.

La unión de D con A, nos determina la media proporcional x.

5) Equivalencia

Se dice que dos figuras son equivalentes, cuando sus superficies son iguales, aunque su forma sea distinta.

a) Dado un triángulo A, B, C, cualquiera dibujar otro equivalente. Fig. 1

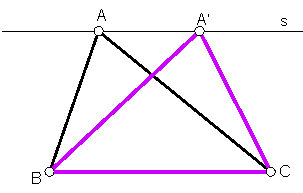
Fig. 1

Se traza por el vértice opuesto a la base del triángulo una línea paralela a esta. Cualquier punto A´ trazado en esta paralela unido con los vértices de la base determina un triángulo equivalente al propuesto.

Como los dos triángulos tienen la misma base y altura tienen la misma superficie.

b) Construir un poligono equivalente a uno dado con un lado menos.

ABCDE es el polígono dado. Trazar al mismo la diagonal AC y por el vértice B una paralela a dicha diagonal, la cual cortará en F a la prolongación del lado CD. El polígono es equivalente al dado. 

Al polígono propuesto se le ha restado el triángulo ABC y sumado ACF los cuales son equivalentes por tener la misma base y altura 

c/ Dado un polígono cualquiera de vértices a, b, c, d, f, g, dibujar otro con dos lados menos. Fig. 1.

Nos basamos en el ejercicio anterior.

Unimos el vértice –D - con – B –

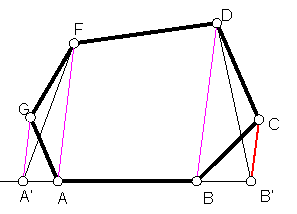
Fig. 1

Trazamos por C una paralela al lado  – DB – y  donde se corte con la prolongación del lado – ABnos determina el punto - B’-.

Unimos – B’ – con –D - y tenemos un lado menos.

Repetimos la operación con los vértices A, G, F.

d) Dibujar el cuadrado equivalente al triángulo, A, B, C. Fig. 1

Bastará con resolver una pequeña ecuación:

Superficie del cuadrado Sc = L*L

Superficie del triángulo   St = ½ b * h

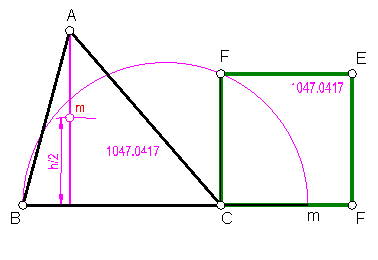
Fig. 1

Igualamos las áreas L*L = ½ h * b

De acuerdo con lo anterior, hallamos el segmento media proporcional entre la mitad de la altura del triángulo su base.

El segmento – CF- será el lado que buscamos.

d2) Dibujar el triángulo equivalente al cuadrado.

Se toma uno de los lados AB del cuadrado como va se concentró en su punto medio o se describe la circunferencia que contiene a los vértices opuestos
A partir del vértice B se lleva sobre lado BC una longitud BF igual al doble de la distancia de que media entre el vértice B y el extremo correspondiente de la circunferencia.
Cualquier punto ( el M por ejemplo) de la paralela trazada a la base por F nos define el vértice superior del triángulo equivalente cuya base es el segmento GB


BF, altura del triángulo , es igual a 2BE. El área del cuadrado es A B x BC =BC cuadrado. Pero dado que BC es la media proporcional entre los segmentos GB y BE podemos escribir S=BC2=GBxBE.

e) Dado un pentágono A, B, C, D, E, dibujar el triángulo equivalente. Fig. 1.

Unimos el vértice – C - con – E –

Prolongamos el lado -AE –

Trazamos  por D la paralela – D E’.

Unimos –C- con –E’-.

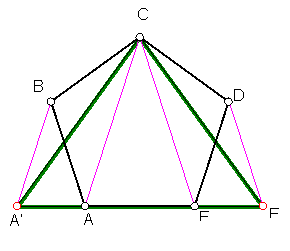
Fig. 1

Repetimos la operación para el triángulo -ABC-.

5.1. Sección áurea de un segmento

Fig. 1

Denominamos sección áurea del segmento AC, a la

división que se produce en el mismo, de tal forma que la relación existente entre la parte mas pequeña y la mas grande es la misma que la existente entre la mas grande y su totalidad. Fig. 1.

a/x = x/b

a) Hallar la división áurea de un segmento dado. Fig. 1.

Sea el segmento AB.

Fig. 1

Por el extremo B, trazamos una recta perpendicular.

Sobre dicha perpendicular llevamos la mitad del segmento  AB, punto m, que corta a la perpendicular en C.

Unimos A con C, y haciendo centro en C y con radioCB, trazamos un arco que corta a la recta AC en D.

Por último, con centro en A trazamos el arco AE, parte áurea

del segmento AB.

b) Dado un cuadrado, dibujar el rectángulo áureo. Fig. 1.

El rectángulo cuyos lados están relacionados según la proporción áurea, se denomina rectángulo áureo.

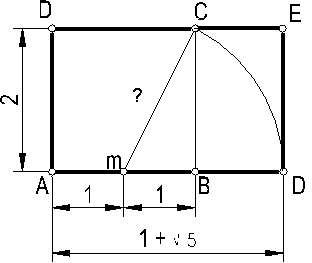
Fig. 1.

Este es un rectángulo especial armonioso en sus proporciones. Los egipcios conocían esta proporción y la usaron en arquitectura. Los Griegos también la usaron en sus construcciones, por ejemplo El Partenón. Las dimensiones del D.N.I, están en proporción áurea. En España, en la Alhambra, el Escorial y otros muchos

edificios se ha tenido en cuenta. Fig. 2.

Partimos de un cuadrado cualquiera de lado 2unidades vértices A, B, C, D.

Fig. 2

Hallamos la mediatriz del lado que valdrá 1, punto m. Se demuestra fácilmente que m C, vale  √5. Haciendo centro en m, trazamos un arco, que corta a la prolongación de lado en D.El segmento AD será igual a 1+ √ 5 , por tanto la proporción entre los dos lados vale (1+ √ 5)/2 = 1,61803. A este número se le llama Número de oro.

Lo obtuvieron los griegos al hallar la relación entre la diagonal de pentágono y el lado.

c) Dado del rectángulo, hallar el otro, de tal forma que estén en proporción áurea. Fig. 1.

Partimos del lado AB del rectángulo

Hallamos su mediatriz, punto m.

Fig. 1

Trazamos la perpendicular en el extremo A y B.

Haciendo centro en B, trazamos el arco mC.

Unimos A con C.

Haciendo centro en C, trazamos el arco BD.

Y por último haciendo centro en A, trazamos el arcoAD, que nos determina el lado menor del rectángulo áureo.

5.2 Cuadratura del círculo.
Hay varios métodps este es uno de ellos. Todos son aproximados.

Se divide el diámetro del círculo  en 7 partes iguales
y con centro en los extremos A y B trazar arcos de radio 4/7 y 3/7 del diámetro respectivamente obteniendo los puntos D y C sobre las prolongaciones del diámetro.
Trazar una semicircunferencia de radio CD, levantando por A una perpendicular hasta cortar en E a la semicircunferencia. El segmento AE es el lado del cuadrado equivalente al círculo del diámetro dado AB.

AE es media proporcional entre los segmentos CA y AD. Podemos decir que: